Question

What is the vertex of the graph of this function

y= -(x-1)(x+3)​

Answer 1

Vertex = (-1,4).

Explanation:

Given equation is
`y=-(x-1)(x+3)`.

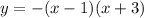Now we need to find the vertex of the graph of given function
`y=-(x-1)(x+3)`.

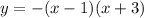To find that we can rewrite given function into vertex form

`y=-(x-1)(x+3)`

`y=-(x^2+3x-1x-3)`

`y=-(x^2+2x-3)`

`y=-(x^2+2x+1-1-3)`

`y=-((x+1)^2-1-3)`

`y=-((x+1)^2-4)`

`y=-(x+1)^2+4`

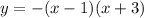
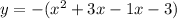
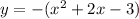
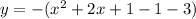
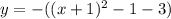
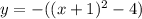
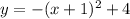
Now compar this equation with
`y=a(x-h)^2+k`

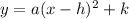
we get: h=-1, k=4

Hence vertex is (h,k) or (-1,4).