Question

Find the LCM of m^2 - 4m - 5 and m^2 + 8m + 7

Answer 1

LCM=(m+1)(m-5)(m+7)

Explanation:

Given expressions are
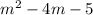`m^2-4m-5` and
`m^2+8m+7`.

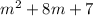To find the LCM, first we need to find factors of both expressions.

`m^2-4m-5`

`=m^2+1m-5m-5`

`=m(m+1)-5(m+1)`

`=(m+1)(m-5)`

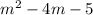
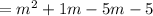
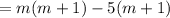
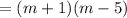
Similarly factor other expression

`m^2+8m+7`

`=(m+1)(m+7)`

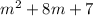
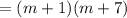
Common factor in both is (m+1)

bring down remaining non-common factors.

So LCM=(m+1)(m-5)(m+7)