Answer:
D)
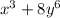
Explanation:
We have been given four choices.
A)
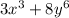
B)
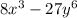
C)
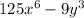
D)
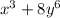
Now we need to find about which of the above choices is a sum of cubes.
Basically we need to check which one of the given choices can be represented in cubic form along with addition sign.
3 and 9 can't be written in cubic form unless we use radical numbers.
So the only choice left is D)
D)
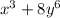
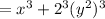

which is clearly visible as sum of cubes.