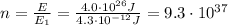Question

assume the suns total energy output is 4.0 * 10^26 watts, and 1 watt is 1 joule/second. assume 4.3 * 10^-12 J is released from each p-p chain of reactions. use the energy yield from the proton-proton chain to determine how many proton-proton chain reactions must be happening each second in the solar core

Answer 1

`9.3\cdot 10^(37)`

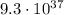
Step-by-step explanation:

Power is defined as the energy produced (E) per unit of time (t):

`P= (E)/(t)`

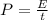
This means that the energy produced in the Sun each second (1 s), given the power
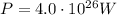`P=4.0\cdot 10^(26)W`, is

`E=Pt=(4.0\cdot 10^(26)W)(1s )=4.0\cdot 10^(26) J`

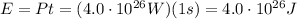
Each p-p chain reaction produces an amount of energy of

`E_1 = 4.3\cdot 10^(-12) J`

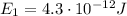
in order to get the total number of p-p chain reactions per second, we need to divide the total energy produced per second by the energy produced by each reaction:

`n=(E)/(E_1)=(4.0\cdot 10^(26) J)/(4.3\cdot 10^(-12) J)=9.3\cdot 10^(37)`