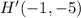Question

If the following figure is rotated 90° counterclockwise about the origin, what is the new location? ​

Answer 1

Answer: Last option.

Explanation:

We need to apply the Rule for 90° counterclockwise rotation about the origin. Given a point
`P(x,y)`:

`P(x,y)` →
`P'(-y,x)`

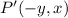
We can observe in the figure that the coordinates of the points E, F, G and H are:

`E (2,6)`

`F(7,-4)`

`G(-2,-7)`

`H (-5,1)`

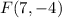
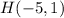
Then, applying the rule, we get the coordinates of the new location of the figure EFGH:

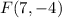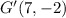
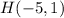`E (2,6)` →
`E'(- 6,2)`

`F(7,-4)` →
`F'(4,7)`

`G(-2,-7)` →
`G'(7,-2)`

`H (-5,1)` →
`H'(-1,-5)`