Question

Solve the system of equations using elimination. –9x – 2y = –115 –6x + 2y = –110

Answer 1

(15,-10)

Step-by-step explanation

The given equations are:

–9x – 2y = –115 ...(1)

–6x + 2y = –110...(2)

Add equation (1) from equation (2) to eliminate y.

-9x+-6x=-110+-115

This implies that,

-15x=-225

Divide both sides by -15

`x = 15`

Put the value of x into equation (2) to find y.

`- 6(15 ) + 2y = - 110`

`- 90+ 2y = - 110`

`2y = - 110 + 90`

`2y = - 20`

`y = - 10`

The solution is (15,-10)

Answer 2

Hello!

The answers are:

`x=15\\y=-10`

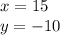
Why?

Solving systems of equations using elimination means multiplying/dividing the factors of the given equations in order to reduce variables and make the isolating process simpler, so, solving we have:

We are given the equations:

`\left \{ {{-9x-2y=-115} \atop {-6x+2y=-110}} \right.`

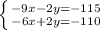
We have that the terms that contains the variable "y" are equal with opposite signs, so, we can eliminate both directly, and then, isolate the variable "x", so, solving we have:

`\left \{ {{-9x-2y=-115} \atop {-6x+2y=-110}} \right\\\\\left \{ {{-9x=-115} \atop {-6x=-110}} \right\\\\-9x-6x=-115-110\\\\-15x=-225\\\\x=(-225)/(-15)=25`

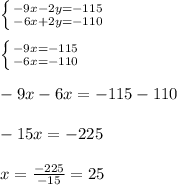
Now, that we know "x" we need to substitute it into any of the given equations in order to find "y", so, substituting we have:

`-9x-2y=-115\\\\-9*(15)-2y=-115\\\\-135+115=2y\\\\2y=-20\\\\y=(-20)/(2)=-10`

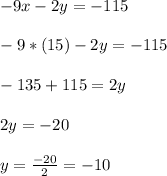
Hence, we have that:

`x=15\\y=-10`

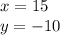
Have a nice day!