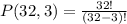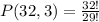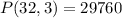Answer:
There are 29760 possible ways
Explanation:
Mrs. Pearson must elect a President, a Vice President and a Treasurer. Then you must choose 3 people. In this case the order matters, because there are three different positions (President, Vice President and Treasurer)
So this is a problem of perm
So this is a problem of permutations. The formula to calculate a permutation is:
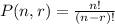
Where n is the total number of people and you can choose r of them
So: