Question

Three ships are at sea: the Admiral, the Barstow, and the Cauldrew. The crew on the Admiral can see both the Barstow and the Cauldrew. They measure the angle between the line of sight to the Barstow and the line of sight to the Cauldrew as 31°. They radio the Barstow and by comparing known landmarks, find that the distance between the Admiral and the Barstow is 402 meters. The Barstow reports that an angle of 70° is found between their line of sight to the Admiral and their line of sight to the Cauldrew. To the nearest meter, what is the distance between the Barstow and the Cauldrew?

38 meters

211 meters

220 meters

133 meters

Answer 1

I am very disappointed in you. I give you extra credit to try and help your grade and you cheat? Please come and see me tomorrow about what you are doing.

Explanation:

Answer 2

211 meters

Explanation:

Let A represents the Admiral, B represents the Barstow and C represents the Cauldrew.

According to the question,

AB = 402,

∠B = 70°,

∠A = 31°,

∵ ∠B + ∠A + ∠C = 180° ⇒ 70° + 31° + ∠C = 180° ⇒ ∠C = 180° - 101° = 79°

By the law of sine,

`(sin C)/(AB)=(sin A)/( BC)`

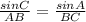
By substituting the values,

`(sin 79^(\circ))/(402)=(sin 31^(\circ))/(BC)`

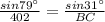
By cross multiplication,

`BC* sin 79^(\circ) = 402* sin 31^(\circ)`

`\implies BC = ( 402* sin 31^(\circ))/(sin 79^(\circ))=210.92050995\approx 211`

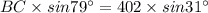
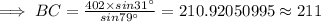
Hence, the distance between the Barstow and the Cauldrew is 211 meters ( approx )

Second option is correct.