Hello!
The answer is:
The general form of the circle is:
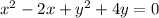
Why?
We are given the standard form of a circle, so, to calculate the general form, we need to solve notable products.
We must remember the way to solve the notable product:
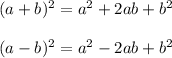
So,
We are given the equation:
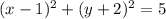
Then, solving the notable products, and adding/subtracting like terms, we have:
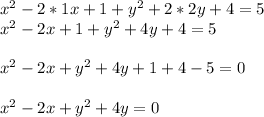
Hence, have that the general form of the circle is:
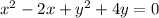
Have a nice day!