Question

The population of a heard of cattle numbered was 5000 to begin with and was 10,000 after 10 years. If the population was growing exponentially, what was the growth rate? show all work

A) r=2
B) r=20
C)r=0.69
D)r=6.9

Answer 1

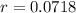`r=0.0718`. The closest value from your given choices is C)r=0.69

Explanation:

To solve this we are using the standard exponential growth equation:

`f(t)=A(1+r)^t`

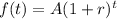
where

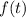`f(t)` is the final population after
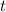`t` years

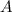`A` is the initial population

`r` is the growth rate in decimal form

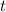`t` is the time in years

We know from our problem that the initial population is 5000, the final population is 10000, and the time is 10 years, so
`A=5000`,
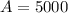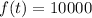`f(t)=10000`, and
`t=10`.

Let's replace the values and solve for
`r`:

`f(t)=A(1+r)^t`

`10000=5000(1+r)^(10)`

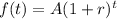
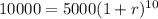
Divide both sides by 5000

`(10000)/(5000) =(1+r)^(10)`

`2=(1+r)^(10)`

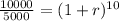
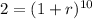
Take root of 10 to both sides

`\sqrt[10]{2} =\sqrt[10]{(1+r)^(10)}`

`\sqrt[10]{2} =1+r`

Subtract 1 from both sides

`\sqrt[10]{2}-1=r`

`r=\sqrt[10]{2}-1`

`r=1.0718-1`

`r=0.0718`

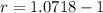
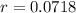
We can conclude that the growth rate of our exponential equation is
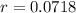`r=0.0718`. The closest value from your given choices is C)r=0.69