bearing in mind that perpendicular lines have negative reciprocal slopes hmmmmm wait a second, what's the slope of that line above anyway?
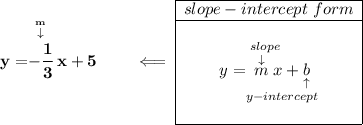
therefore any perpendicular line to that
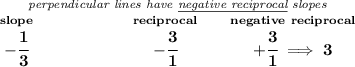
so, we're really looking for the equation of a line whose slope is 3 and runs through (1, -10)
