Hello!
The answer is:
The ball will hit the ground in 7.69 seconds.
Why?
To solve this problem, we need to apply the following projectile motion equation:
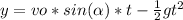
To calculate when the ball wil hit the ground, in other words the time of flight, we need to make "y" equal to 0, and considerate the initial height, so, we have:
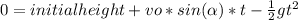
Then, we are given the following information:
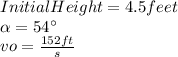
Now, substituting and solving, we have:
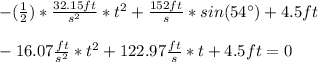
We have a quadratic equation, where:
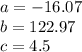
Now, using the quadratic equation to find the values of "t" , we have:
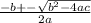
Substituting we have:


Therefore, since the time cannot be negative, we have to discard "t1", so, the answer is: 7.69 seconds
Hence, the ball will hit the ground in 7.69 seconds.
Have a nice day!