Hello!
The answer is:
The speed of the wind is 150mph.
Why?
To calculate the speed of the wind, we need to write two equations using the given information about the speed when the airplane was traveling with the wind and against the wind, considering that it travel the same length of time.
So, writing the equations, we have:
Traveling with the wind:
We know that the speed of the airplane is 325 mph and it travels 1360 miles with the wind, so, for the equation, we have:
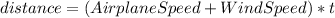
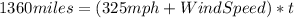
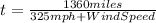
Traveling against the wind:
We know that the speed of the airplane is 325 mph and it travels 1240 miles with the wind, so, for the equation, we have:
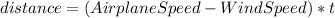
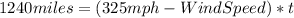
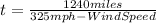
Then, making making equal the time, we have:
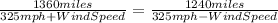

Hence, we have that the speed of the wind is 150mph.
Have a nice day!