Question

What is the vertex of the function f(x) = x2 + 12x?

0 (6-36)
(6.0)
(6.0)
(6 -36)
Mark this and retum
Save and Exit
SUR

Answer 1

(-6,-36)

Explanation:

The given function is

`f(x)=x^2+12x`

We complete the square to write this function in the vertex form.

Add and subtract the square of half the coefficient of x.

`f(x)=x^2+12x+6^2-6^2`

`f(x)=x^2+12x+36-36`

The first three terms is now a perfect square trionomial

`f(x)=(x+6)^2-36`

Or

`f(x)=(x--6)^2-36`

The function is now in the form:

`f(x)=a(x-h)^2+k`

where h=-6 and k=-36

The vertex is therefore (h,k)=(-6,-36)

Answer 2

(-6, -36)

Explanation:

The vertex
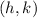`(h,k)` of a function of the form
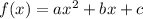`f(x)=ax^2+bx+c` is given by the formula:

`h=(-b)/(2a)`

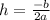
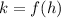`k=f(h)` in other words, we find h and then evaluate function at h to find k.

We know from our function that
`a=1`,
`b=12`.

Replacing values

`h=(-12)/(2(1))`

`h=-(12)/(2)`

`h=-6`

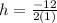
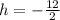
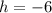
Now we can evaluate our function at -6 to find k:

`k=f(h)=f(-6)`

`k=(-6)^2+12(-6)`

`k=36-72`

`k=-36`

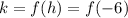
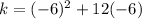
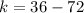
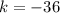
We can conclude that the vertex (h, k) of our function is (-6, -36)