Question

Mrs. Robinson, an insurance agent, earns a salary of $4,800 per year plus a 3% commission on her sales. The average price of a policy she sells is $6,100.

Write an inequality to find how many policies Mrs. Robinson must sell to make an annual income of at least $8,000.

4800+183x<(line under the arrow)=8000
4800+183x=8000
4800+183x>=8000
4800+186>(ine under the arrow)=8000

Answer 1

`4800+183x\geq 8000`

She must sell at least 18 policies to make an annual income of at least $8,000

Explanation:

Let
`x` be the number of policies Mrs. Robinson must sell

We know that Mrs. Robins makes 3% on commission for each policy sold. We also know that the average price of a policy is $6,100, so she makes 3% of $6,100 per policy sold. To find the 3% of $6,100 we just need to multiply 3% and $6,100; then dive the result by 100%:

`(3*6,100)/(100) =183`

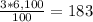
Now we know that she makes $183 per policy sold. Since
`x` is the number of policies sold,
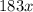`183x` is her total commission for selling
`x` policies.

We also know that She makes $4,800 per year, so her total annual income is her salary plus her commissions, in other words:

`4800+183x`

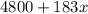
Finally, we know that she wants to make at least $8,000, so her salary plus her commissions must be greater or equal than $8,000:

`4800+183x\geq 8000`

Let's solve the inequality:

1. Subtract 4800 from both sides

`4800-4800+183x\geq 8000-4800`

`183x\geq 3200`

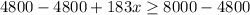
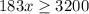
2. Divide both sides by 183

`(183x)/(183) \geq (3200)/(183)`

`x\geq 17.48`

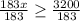
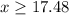
Since she can't sell a fraction of a policy, we must round the result to the next integer:

`x\geq 18`

We can conclude that she must sell 18 policies to make an annual income of at least $8,000.