Question

A fireplace contains 72 bricks along its bottom row. If each row above decreases by 6 bricks, what is the function that shows the bricks on the 14th row?

Answer 1

`a_n=78-6n`

`a_(14)=78-6(14)`

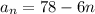
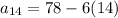
Explanation:

To solve this, we are using the formula for the nth term of an arithmetic progression:

`a_n=a_1+(n-1)d`

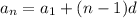
where

`a_1` is the first term of the progression

`d` is the difference

`n` is position of the term in the progression

We know for our problem that the bottom row contains 72 bricks, so
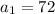`a_1=72`. We also know that each row above decreases by 6 bricks, so the difference is -6 (
`d=-6`).

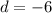Replacing the values:

`a_n=72+(n-1)(-6)`

`a_n=72-6n+6`

`a_n=72-6n+6`

`a_n=78-6n`

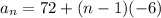
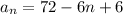
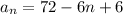
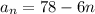
Where
`n` is the row

Since we want to now the number of bricks in the 14th row,
`n=14`:

`a_(14)=78-6(14)`

`a_(14)=78-84`

`a_(14)=-6`

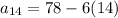
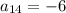
Since bricks can't be negative, we can conclude that this is an impossible real-life situation.