Answer: The required values are
u = 140, v = 28, w = 40, x = 40 and y = 20.
Step-by-step explanation: We are given to find the values of u, v, w, x and y from the figure shown.
We see that
the lines AB and CD are parallel to each other and PS is a transversal.
So, we must have
![u^\circ=140^\circ~~~~\textup{[alternate interior angles]}\\\\\Rightarrow u=140.](https://img.qammunity.org/2020/formulas/mathematics/middle-school/5uf0v5li1rrypifd11la4zj24zukrq8u7w.png)
Now, we also have
![u^\circ=5v^\circ~~~~~\textup{[vertically opposite angles]}\\\\\Rightarrow u=5v\\\\\Rightarrow 140=5v\\\\\Rightarrow v=(140)/(5)\\\\\Rightarrow v=28.](https://img.qammunity.org/2020/formulas/mathematics/middle-school/t1cy6ry2gskhkqt8oajrstvlqrvyfbwyv4.png)
Now, from the property of linear pair, we get
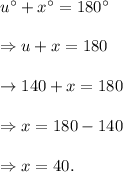
Since angles of measure w° and x° are alternate interior angles, so

Again, by using the property of linear pair, we get

Thus, the required values are
u = 140, v = 28, w = 40, x = 40 and y = 20.