Question

The Gross National Product (GNP) is the value of all the goods and services produced in an economy, plus the value of the goods and services imported, less the goods and services exported. During the period 1994-2004, the GNP of Canada grew about 4.8% per year, measured in 2003 dollars. In 1994, the GNP was $5.9 billion.

Assuming this rate of growth continues, in what year will the GNP reach $10 trillion?

A. 2103
B.2152
C. 2164
D.2168

Answer 1

B.2152

Explanation:

To solve this we are using the standard exponential growth equation:

`y=a(1+b)^x`

where

`y` is the final value after
`x` years

`a` is the initial value

`b` is the growing rate in decimal form

`x` is the time in years

We know from our problem that the GNP is growing 4.8% per year, so
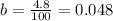`b=(4.8)/(100) =0.048`. We also know that the GDP in 1994 was $5.9 billion and the desired GNP is $10 trillion, so
`a=5,900,000,000` and
`y=10,000,000,000,000`.

Replacing values

`y=a(1+b)^x`

`10,000,000,000,000=5,900,000,000(1+0.048)^x`

`10,000,000,000,000=5,900,000,000(1.048)^x`

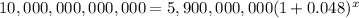
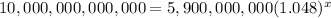
Divide both sides by 5,900,000,000:

`(10,000,000,000,000)/(5,900,000,000) =(1.048)^x`

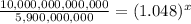
Take natural logarithm to both sides

`ln(1.048)^x=ln((10,000,000,000,000)/(5,900,000,000))`

`xln(1.048)=ln((10,000,000,000,000)/(5,900,000,000))`

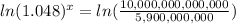
Divide both sides by ln(1.048)

`x=(ln((10,000,000,000,000)/(5,900,000,000)))/(ln(1.048))`

`x` ≈ 158

We now know that Canada's GNP will reach $10 trillion after 158 years from 1994, so to find the year we just need to add 158 years to 1994:

1994 + 158 = 2512

We can conclude that the correct answer is B.2152