Answer:
The graph touches the x-axis at (–2.5, 0).
Explanation:
Given : f(x) = 4x² + 20x + 25.
To find : Which statement describes the graph .
Solution : We have given
f(x) = 4x² + 20x + 25.
On factoring
4x² + 10x + 10x+ 25 = 0
On taking common 2x from first two terms and 5 from last two terms.
2x ( 2x + 5 ) +5 (2x + 5 ) = 0
On grouping
(2x +5) (2x +5) = 0
For 2x +5 = 0
On subtracting 5 both side
2x = -5
On dividing by 2
x =
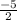 = - 2.5
= - 2.5
x = - 2.5 .
Points (-2.5 , 0)
Therefore, The graph touches the x-axis at (–2.5, 0).