Question

(3⁵)²/3⁻²

A. 3¹⁰

B. 3¹²

C.
`3^(9)`

D.
`3^(8)`

Answer 1

B. 3¹²

Explanation:

To solve this we need to apply the following laws of exponents:

1.
`(a^n)^m=a^(n*m)`

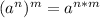
2.
`a^(-n)=(1)/(a^n)`

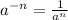
Let's apply the first law to the numerator of our fraction and the second law to the denominator. For the numerator,
`(3^5)^2`,
`a=3`,
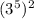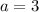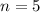`n=5`, and
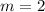`m=2`. For the denominator
`3^(-2)`,
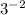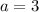`a=3` and
`n=-2`

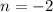
Replacing values

`((3^5)^2)/(3^(-2)) =(3^(5*2))/((1)/(3^2) ) =(3^(10))/((1)/(3^2) )`

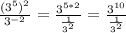
Now, remember that to divide fractions we just need to invert the order of the second fraction and multiply:

`(3^(10))/((1)/(3^2) )=3^(10)*(3^2)/(1) =3^(10)*3^2`

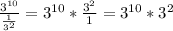
Finally, we can use the law of exponents for multiplication to get our answer:

`a^n*a^m=a^(n+m)`

`3^(10)*3^2=3^(10+2)=3^(12)`

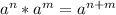
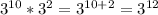
We can conclude that the correct answer is B. 3¹²