Question

Please show work on these questions!!!

Find the radian measure of an angle of -280 degrees.

Find the degree measure of an angle of 3pi/5 radians.

Find the exact values of cos(3pi/4 radians) and sin(3pi/4 radians).

Answer 1

- 14π/9; 108°; -√2/2; √2/2

Explanation:

To convert from degrees to radians, use the unit multiplier
`(\pi )/(180)`

In equation form that will look like this:

- 280° ×
`(\pi )/(180)`

Cross canceling out the degrees gives you only radians left, and simplifying the fraction to its simplest form we have
`-(14\pi )/(9)`

The second question uses the same unit multiplier, but this time the degrees are in the numerator since we want to cancel out the radians. That equation looks like this:

`(3\pi )/(5)` ×
`(180)/(\pi )`

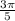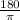
Simplifying all of that and canceling out the radians gives you 108°.

The third one requires the reference angle of
`(3\pi )/(4)`.

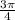If you use the same method as above, we find that that angle in degrees is 135°. That angle is in QII and has a reference angle of 45 degrees. The Pythagorean triple for a 45-45-90 is (1, 1, √2). But the first "1" there is negative because x is negative in QII. So the cosine of this angle, side adjacent over hypotenuse, is
`-(1)/(√(2) )`

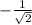
which rationalizes to
`-(√(2) )/(2)`

The sin of that angle is the side opposite the reference angle, 1, over the hypotenuse of the square root of 2 is, rationalized,
`(√(2) )/(2)`

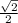
And you're done!!!