Answer:
The third side must be smaller than 20 inches and greater than 4 inches
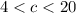
Explanation:
Let a, b and c be the lengths of triangle's sides. Then
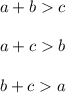
Use this rule in your case. So, if a=12 and b=8, then
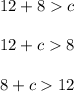
Hence, you get

From these inequalities, you can state that
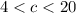
So, c must be smaller than 20 inches and greater than 4 inches.