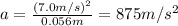a. 7.0 m/s
First of all, we need to convert the angular speed (1200 rpm) from rpm to rad/s:
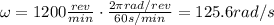
Now we know that the row is located 5.6 cm from the centre of the disc:
r = 5.6 cm = 0.056 m
So we can find the tangential speed of the row as the product between the angular speed and the distance of the row from the centre of the circle:
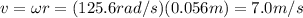
b.
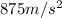
The acceleration of the row of data (centripetal acceleration) is given by
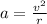
where we have
v = 7.0 m/s is the tangential speed
r = 0.056 m is the distance of the row from the centre of the trajectory
Substituting numbers into the formula, we find