Question

Given the system of equations:

2x – y = –2
x = 14 + 2y

Answer the following:
A) What is the value of the system determinant?
B) What is the value of the y−determinant?
C) What is the value of the x−determinant?
D) What is the solution to the system of equations?

My mind is blank when I look at this, any help will be appreciated.

Answer 1

2x - y = -2

x = 14 + 2y

2x - y = -2

x - 2y = 14

The system determinant = -3

2 (-2) - 1 (-1)

-4 + 1

-3

The y-determinant = 30

(14) - 1 (-2)

28 + 2

30

The x-determinant = 18

-2 (-2) - 14 (-1)

4 + 14

18

The solution is x = -6 and y = -10 or (-6,-10)

x = 18/-3

x = -6

y = 30/-3

y = -10

Answer 2

The determinant of A (the main matrix) is -3; the determinant of y is 30; the determinant of x is 18; the solution to the system is (-6, -10)

Explanation:

Set up the matrix to find the determinant of the main matrix. Find the determinant by multiplying the numbers on the major axis and subtract from that the multiplication of the numbers on the minor axis:

`\left[\begin{array}{ccc}2&-1&\\1&-2\\\end{array}\right]`

Find the determinant by multiplication:

(2×-2)-(1×-1)= -3

To find the determinant of y, replace the second column with the solutions to have a matrix that looks like this:

`\left[\begin{array}{ccc}2&-2\\1&14\\\end{array}\right]`

To find the determinant of that matrix by multiplication:

(2×14)- (1× -2) = 30

Lastly, find the determinant of x by replacing the first column with the solutions. That matrix will look like this:

`\left[\begin{array}{ccc}-2&-1\\14&-2\\\end{array}\right]`

Find the determinant of x by multiplication:

(-2 × -2) - (14 × -1) = 18

Now we want Cramer's Rule that tells us if we divide the determinant of
`A_(x)`

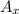
by the determinant of A, we will find the value of x:

`(A_(x) )/(A)=(18)/(-3)  =-6`

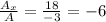
and the same for y:

`(A_(y) )/(A)=(30)/(-3)=-10`

So the solution to the system is (-6, -10)