Answer:
a = 4, b = 3, and c = -3
Explanation:
A quadratic equation of a variable is an equation that has the general form of:
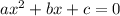 ,
,
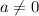
Where x is the variable, and a, b and c constants; a is the quadratic coefficient (other than 0), b the linear coefficient and c is the independent term. This polynomial can be interpreted by means of the graph of a quadratic function, that is, by a parabola. This graphical representation is useful, because the abscissas of the intersections or point of tangency of this graph, in the case of existing, with the X axis are the real roots of the equation. If the parabola does not cut the X axis the roots are complex numbers, they correspond to a negative discriminant.
So, the coefficients are a = 4, b = 3, and c = -3