Answer:
{x while x ≠2, -2}
Explanation:
First let's define domain,
Domain is the set of all values on which the function is defined i.e. the function doesn't approach to infinity.
Given function is:
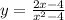
We will look for all the values of x on which the function will become undefined:
We can see that x= 2 and x=-2 will make the denominator zero as there is x^2 involved. The denominator zero will make the function undefined.
So, the domain of the function is set of all real numbers except 2 nd -2 {x while x ≠2, -2} ..