Question

A cell-phone company has noticed that the probability of a customer experiencing a dropped call decreases as the customer approaches a cell-site base station. A company representative approached a cell site at a constant speed and calculated the probability of a dropped call at regular intervals, and the probabilities formed the geometric sequence 0.8, 0.4, 0.2, 0.1, 0.05. If the company representative continues calculating the probability of a dropped call, what will be the next term in the sequence?

Answer 1

the answer is 0.00221184

Explanation:

as we can see 3rd term is product of first two terms

4th term is product of third and second term

5th term is the product of fourth and third term

the next term in the sequence which is the sixth term will be the product of fifth and fourth term

Answer 2

The next term of geometric sequence is 0.025 which is the probability of dropped call.

Explanation:

We are given the following information in the question:

The probability of a customer experiencing a dropped call decreases formed the geometric sequence.

The geometric sequence is:

0.8, 0.4, 0.2, 0.1, 0.05

First term = a = 0.8

Common difference = r =
`(a_(n))/(a_(n-1)) = (0.4)/(0.8) = (1)/(2)`

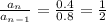
We have to find the next term of the geometric series to find the next probability.

Next term of sequence =

`a_n = a_(n-1)* r\\= 0.05* \displaystyle(1)/(2)\\\\= 0.025`

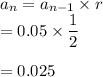
Hence, the next term of geometric sequence is 0.025 which is the probability of dropped call.