Answer:
B
Explanation:
The standard form of a circle is
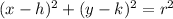
where h and k are the coordinates of the center of the circle and the radius is squared. The radius is easy...take the square root of 25 to get that the radius is 5. Since the pattern for the standard form is "x-" and "y-", if (x+2)^2 is the horizontal placement of the center, it actually was originally written as (x-(-2))^2, so the h coordinate is -2. Same goes for the vertical movement of the center. (y-(5))^2 means that the k coordinate is a positive 5.