Answer:
D)4x + 6/(x + 1)(x - 1)
Explanation:
A field is basically a rectangle, so to find the perimeter of our field we are using the formula for the perimeter of a rectangle
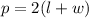
where
 is the perimeter
is the perimeter
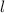 is the length
is the length
 is the width
is the width
We know from our problem that the field has length 2/x + 1 and width 5/x^2 -1, so
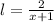 and
and
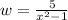 .
.
Replacing values:
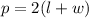
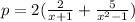
Notice that the denominator of the second fraction is a difference of squares, so we can factor it using the formula
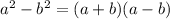 where
where
 is the first term and
is the first term and
 is the second term. We can infer that
is the second term. We can infer that
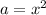 and
and
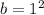 . So,
. So,
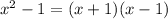 . Replacing that:
. Replacing that:
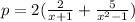

We can see that the common denominator of our fractions is
 . Now we can simplify our fraction using the common denominator:
. Now we can simplify our fraction using the common denominator:

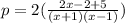
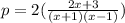
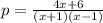
We can conclude that the perimeter of the field is D)4x + 6/(x + 1)(x - 1).