Question

How many real number solutions does the equation have. Y=3x^2-5x-5

Answer 1

2

Explanation:

To find how many real solution a quadratic equation has, we just need to find the value of its discriminant. If the discriminant is zero, the quadratic only has one real solution; if the discriminant is positive, the quadratic has two real solution; if the discriminate is negative, the quadratic doesn't has any real solutions.

The discriminant of a quadratic equation of the form
`ax^2+bx+c` is given by:
`b^2-4ac`

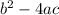
We know from our quadratic that
`a=3`,
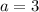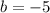`b=-5`, and
`c=-5`.

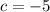Replacing values:

`(-5)^2-4(3)(-5)`

`25+60`

`85`

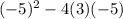
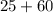
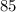
Since the discriminant is positive, we can conclude that our quadratic equation has two real solutions.