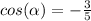Question

If tan=-4/3 in quadrent 2 what is cos​

Answer 1

-3/5

Explanation:

Answer 2

`-(3)/(5)`

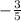
Explanation:

Remember that the tangent trigonometric ratio is the opposite side of right triangle divided by the adjacent side:

`tan(\alpha )=(opposite-side)/(adjacent-side)`

`tan(\alpha )=-(4)/(3)`

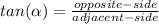
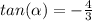
Comparing the equations we can infer that:

opposite side = 4

adjacent side = 3

Now we can use Pythagoras to find the hypotenuse of our right triangle:

`hypotenuse^2=side^2+side^2`

`hypotenuse^2=4^2+3^2`

`hypotenuse^2=25`

`hypotenuse=√(25)`

`hypotenuse=5`

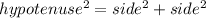
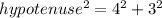
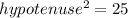
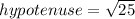
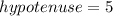
Remember that the cosine trigonometric ratio is the adjacent side divided by the hypotenuse; in other words:

`cos(\alpha)=(adjacent-side)/(hypotenuse)`

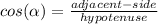
We know that adjacent side = 3 and hypotenuse = 5.

Replacing values:

`cos(\alpha )=(3)/(5)`

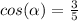
Now, remember that cosine means x and sine means y. In Quadrant 2 x is negative, which means that cosine is negative.

So, if
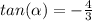`tan(\alpha )=-(4)/(3)` in quadrant 2, then
`cos(\alpha )=-(3)/(5)`