Answer:
16%
Explanation:
To solve this we are using the standard growth equation:

Were
 is the final value after
is the final value after
 years
years
 is the initial value
is the initial value
 is the growth factor (yearly rate of appreciation in our case) in decimal form
is the growth factor (yearly rate of appreciation in our case) in decimal form
 is the time in years
is the time in years
We know from our problem that gold coin appreciated in value from $200.00 to $475.00 in 6 years, so
 ,
,
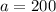 , and
, and
 .
.
Let's replace the values in our equation and solve for
 :
:

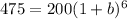
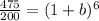
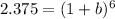
![\sqrt[6]{2.375} =\sqrt[6]{(1+b)^6}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/bj1ydjjitnqgwba4o9yqkvlgt21iksd3px.png)
![1+b=\sqrt[6]{2.375}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kltd44y0v8tn8nw5esfmsy8fizt61aml44.png)
![b=\sqrt[6]{2.375}-1](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ju8src5kka5wzzt7bs0v7y32z0cvvjrlnd.png)
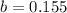
which rounds to

Since our appreciation rate is in decimal form, we need to multiply it by 100% to express it as percentage:
0.16*100% = 16%
We can conclude that the yearly appreciation rate of our gold coin is approximately 16%