Question

Which is the graph of f(x) = (x – 1)(x + 4)?

Answer 1

See attachment.

EXPLANATION

The given function is

f(x) = (x – 1)(x + 4).

This parabola will open upwards because the leading coefficient is positive.

The x-intercepts can be found by equating the function to zero.

`(x - 1)(x + 4) = 0`

By the zero product property;

`x - 1 = 0 \: or \: x + 4 = 0`

This implies that,

`x = 1 \: or \: x = - 4`

The graph that touches the x-axis at -4 and 1, and opens upwards is the last graph.

The correct choice is D.

Answer 2

The fourth graph (last graph)

Explanation:

Remember that the zeros of a function are the x-intercepts of the graph. To find the zeros we just need to set the function equal to zero and solve for x:

`f(x)=(x-1)(x+4)`

`(x-1)(x+4)=0`

`x-1=0,x+4=0`

`x=1,x=-4`

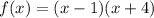
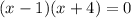
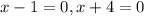
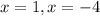
Now we know that the graph or our function intersects the x-axis at x = 1 and x = -4.

Since both x values inside the parenthesis are positive, our parabola is opening upwards.

The only graph opening upwards whose x-intercepts are x = 1 and x = -4 is the fourth one.

We can conclude that the graph of
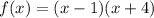`f(x)=(x-1)(x+4)` is the fourth one.