Answer:
# The solution x = -5
# The solution is x = 1
# The solution is x = 6.4
# The solution is x = 4
# The solution is 1.7427
# The solution is 0.190757
Explanation:
* Lets revise some rules of the exponents and the logarithmic equation
# Exponent rules:
1- b^m × b^n = b^(m + n) ⇒ in multiplication if they have same base
we add the power
2- b^m ÷ b^n = b^(m – n) ⇒ in division if they have same base we
subtract the power
3- (b^m)^n = b^(mn) ⇒ if we have power over power we multiply
them
4- a^m × b^m = (ab)^m ⇒ if we multiply different bases with same
power then we multiply them ad put over the answer the power
5- b^(-m) = 1/(b^m) (for all nonzero real numbers b) ⇒ If we have
negative power we reciprocal the base to get positive power
6- If a^m = a^n , then m = n ⇒ equal bases get equal powers
7- If a^m = b^m , then a = b or m = 0
# Logarithmic rules:
1-

2-

3-
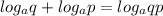
4-
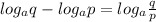
5-
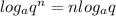
* Now lets solve the problems
#
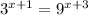
- Change the base 9 to 3²
∴
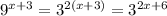
∴
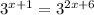
- Same bases have equal powers
∴ x + 1 = 2x + 6 ⇒ subtract x and 6 from both sides
∴ 1 - 6 = 2x - x
∴ -5 = x
* The solution x = -5
# ㏒(9x - 2) = ㏒(4x + 3)
- If ㏒(a) = ㏒(b), then a = b
∴ 9x - 2 = 4x + 3 ⇒ subtract 4x from both sides and add 2 to both sides
∴ 5x = 5 ⇒ divide both sides by 5
∴ x = 1
* The solution is x = 1
#
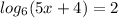
- Use the 1st rule in the logarithmic equation
∴ 6² = 5x + 4
∴ 36 = 5x + 4 ⇒ subtract 4 from both sides
∴ 32 = 5x ⇒ divide both sides by 5
∴ 6.4 = x
* The solution is x = 6.4
#

- Use the rule 3 in the logarithmic equation
∴
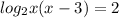
- Use the 1st rule in the logarithmic equation
∴ 2² = x(x - 3) ⇒ simplify
∴ 4 = x² - 3x ⇒ subtract 4 from both sides
∴ x² - 3x - 4 = 0 ⇒ factorize it into two brackets
∴ (x - 4)(x + 1) = 0 ⇒ equate each bract by 0
∴ x - 4 = 0 ⇒ add 4 to both sides
∴ x = 4
OR
∵ x + 1 = 0 ⇒ subtract 1 from both sides
∴ x = -1
- We will reject this answer because when we substitute the value
of x in the given equation we will find
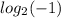 and this
and this
value is undefined, there is no logarithm for negative number
* The solution is x = 4
#
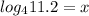
- You can use the calculator directly to find x
∴ x = 1.7427
* The solution is 1.7427
#
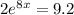 ⇒ divide the both sides by 2
⇒ divide the both sides by 2
∴
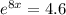
- Insert ln for both sides
∴
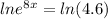
- Use the rule
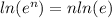 ⇒ ln(e) = 1
⇒ ln(e) = 1
∴ 8x = ln(4.6) ⇒ divide both sides by 8
∴ x = ln(4.6)/8 = 0.190757
* The solution is 0.190757