Question

One pump can fill a tank with oil in 10 hours. Together with a second pump, it can fill the tank in 6 hours. How long will it take the second pump to fill the tank if it is used alone?

Answer 1

The first pump can do 1/0 of the work per hour

Together they do 1/6 of the work per hour

The second alone would do (1/6 - 1/10) of the work per hour.

1/6 - 1/10 = 1/15

The second pump would take 15 hours to do the work.

C) 15

Hope this helps. :)

Answer 2

The second pump can fill a tank with oil in 15 hours.

Explanation:

It is given that one pump can fill a tank with oil in 10 hours. Together with a second pump, it can fill the tank in 6 hours.

Let the second pump can fill a tank with oil in t hours.

One hour work of first pump is
`(1)/(10)`.

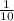One hour work of second pump is
`(1)/(t)`.

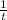One hour work of both pump together is
`(1)/(6)`.

1 hour work of both = 1 hour work of 1st pump + 1 hour work of 2nd pump

`(1)/(6)=(1)/(10)+(1)/(t)`

`(1)/(6)=(t+10)/(10t)`

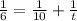
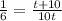
Cross multiply.

`10t=6(t+10)`

`10t=6t+60`

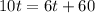
Subtract 6t from both the sides.

`10t-6t=60`

`4t=60`

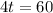
Divide both the sides by 4.

`t=15`

Therefore the second pump can fill a tank with oil in 15 hours.