Question

Use the parabola tool to graph the quadratic function y=−2x2+12x−14 . Graph the parabola by first plotting its vertex and then plotting a second point on the parabola.

Answer 1

(x,12x-18)

Explanation:

Answer 2

Check attached graph

Explanation:

Given equation of the parabola is
`y=-2x^2+12x-14`.

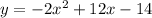Nowe we need to use the parabola tool to graph the quadratic function. Graph the parabola by first plotting its vertex and then plotting a second point on the parabola.

Compare Given equation with
`y=ax^2+bx+c` we get: a=-2 and b=12

then x-coordinate of vertex
`=x=-(b)/(2a)=-(12)/(2\left(-2\right))=3`

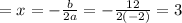
plug x=3 into given function

`y=-2x^2+12x-14`

`y=-2(3)^2+12(3)-14=4`

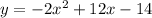
Hence vertex is (3,4).

Plug any x-value say x=0 into given function to find other point

`y=-2(2)^2+12(2)-14=2`

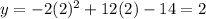
Hence second point is (2,2)

now graph the parabola using both points as shown below: