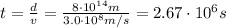Question

An alien spaceship is 8*10^14 m away sends us a radio wave signal. How long does it take for the signal to reach us?

Answer 1

`2.67\cdot 10^6 s`

Step-by-step explanation:

The radio signal travels to us at the speed of light, so at a speed of

`c=3.0\cdot 10^8 m/s`

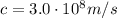
The distance between the spaceship and the Earth is

`d = 8\cdot 10^(14)m`

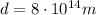
Since the signal travel by uniform motion, we can write

`d = vt`

where

t is the time the signal needs to reach the Earth

By solving the equation for t, we find

`t=(d)/(v)=(8\cdot 10^(14) m)/(3.0\cdot 10^8 m/s)=2.67\cdot 10^6 s`