ANSWER
C.
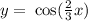
EXPLANATION
The period of a cosine function is calculated using the formula;
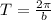
Therefore , if the period is 3π, then
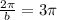
We solve b to obtain,
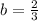
This implies that, the given cosine function must have an equation of the form
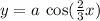
Among the options, the function in this form is:
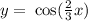
The correct choice is C.