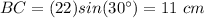Question

In the circle below, DB = 22 cm, and m<DBC = 60°. Find BC. Ignore my handwriting.​

Answer 1

`BC=11\ cm`

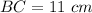
Explanation:

step 1

Find the measure of the arc DC

we know that

The inscribed angle measures half of the arc comprising

`m\angle DBC=(1)/(2)[arc\ DC]`

substitute the values

`60\°=(1)/(2)[arc\ DC]`

`120\°=arc\ DC`

`arc\ DC=120\°`

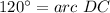
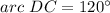
step 2

Find the measure of arc BC

we know that

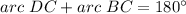`arc\ DC+arc\ BC=180\°` ----> because the diameter BD divide the circle into two equal parts

`120\°+arc\ BC=180\°`

`arc\ BC=180\°-120\°=60\°`

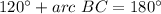
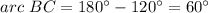
step 3

Find the measure of angle BDC

we know that

The inscribed angle measures half of the arc comprising

`m\angle BDC=(1)/(2)[arc\ BC]`

substitute the values

`m\angle BDC=(1)/(2)[60\°]`

`m\angle BDC=30\°`

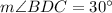
therefore

The triangle DBC is a right triangle ---> 60°-30°-90°

step 4

Find the measure of BC

we know that

In the right triangle DBC

`sin(\angle BDC)=BC/BD`

`BC=(BD)sin(\angle BDC)`

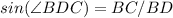
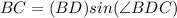
substitute the values

`BC=(22)sin(30\°)=11\ cm`