Question

A test has twenty questions worth 100 points. The test consists of True/False questions worth 3 points each and multiple choice questions worth 11 points each. How many multiple choice questions are on the test? (3 points. 1 point for setting up a correct system of equation, 1 point for the work, 1 point for the correct solution.)

Answer 1

t+m=20--------> t=20-m

3t+11m=100

Substitute

3(20-m)+m=100

60m-3m+11m=100

Get rid of 60

-3m+11m=40

8m=40

Divide by 8

m=5

This tells us that there are 5 Multiple Choice questions. So the remaining 15 question on the test must be True/False questions.

If we got all 5 Multiple Choice questions correct we would score 11 points for each of the five questions and this would give us 55 points. Then if we got all 15 True/False questions correct at 3 points each, we would score 15 times 3 or 45 points. So the total number of points on the test would be 55 + 45 = 100.

Explanation:

Answer 2

Hello!

The answer is:

There are 15 true/false questions while there are 5 multiple choice questions.

Why?

To solve the problem, we need to write two equations using the given information.

We know that there are twenty (20) questions consisting of true/false and multiple choice questions, so, writing the first equation we have:

Let be the true/false questions "x" and the multichoice questions "y".

First equation,

`x+y=20`

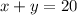
Also, we know that the true/false questions worth 3 points while the multichoice questions worth 11 points making a total of 100 points for the total examen, so, writing the second equation, we have:

Second equation,

`3x+11y=100`

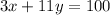
Now, we have to isolate one of the variables in function of the other variable, so, from the first equation, we have:

`x+y=20`

`x=20-y`

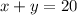
Then, substituting "x" into the second equation, we have:

`3x+11y=100`

`3(20-y)+11y=100`

`60-3y+11y=100`

`60+8y=100`

`8y=100-60=40`

`y=(40)/(8)=5`

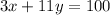
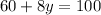
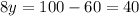
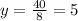
Then, substituting "y" into the first equation, we have:

`x+y=20`

`x+5=20`

`x=20-5=15`

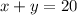
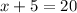
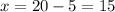
Hence, we have that there are 15 true/false questions while there are 5 multiple choice questions.

Let's prove that we are right by substituting the obtained answers into the both equations, if the equations are satisfied, the answers are ok.

Substituting into the first and the second equation, we have:

First equation,

`x+y=20\\5questions+15questions=20questions\`

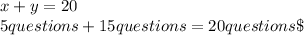
Second equation,

`3x+11y=100points\\3*(15)+11*(5)=100points\\45points+55points=100points`

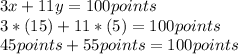
We can see that both equations are satisfied, so, the answers are ok.

Have a nice day!