Question

Shawna can paint a fence in 8 hours. Kevin can paint the same fence in 4 hours. How long will it take them working together? Show all work.

Answer 1

Answer: 2.66 hours

Explanation:

Shawana can paint a fence in 8hours which means in one hour she can paint 1/8 of a fence.

Kevin can paint the same fence in 4 hours, so in one hour he can paint 1/4 of the fence.

Together in 1 hour they can paint 1/8 + 1/4 = 3/8

Total hours for painting is 3/8 or 2.66 hours

Answer 2

Hello!

The answer is:

The will paint the same fence at the same time in 2.67 hours.

Why?

From the statement we know that Shawna can paint a fence in 8 hours while Kevin can paint the same in 4 hours, and we are asked to calculate how long will it take them to paint the fence working together, so, calculating we have:

For Shawna, we have:

`ShawnaRate=(FencePainted)/(TimeToPaint)\\\\ShawnaRate=(1fence)/(8hours)`

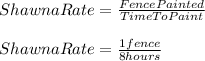
For Kevin, we have:

`KevinRate=(FencePainted)/(TimeToPaint)\\\\KevinRate=(1fence)/(4hours)`

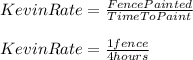
So, the combined work for both Shawna and Kevin will be:

`CombinedWorkRate=(1fence)/(8hours) +(1fence)/(4hours)\\\\CombinedWorkRate=(4fence.hours+8fence.hours)/(32hours^(2))\\ \\CombinedWorkRate=(12fence.hours)/(32hours^(2))\\\\CombinedWorkRate=(12fence.hours)/(32hours^(2))=(3fence)/(8hours)`

Now, if the want to paint the same fence at the same time, we can calculate it by the following way:

`(3fence)/(8hours)=(1fence)/(x(hours))\\\\x=1fence*(8hours)/(3fence)=2.67hours`

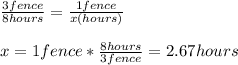
Hence, the will paint the same fence at the same time in 2.67 hours.

Have a nice day!