Question

Help please

must show work

problem 3 and problem 5​

Answer 1

#3. (x-7)(x-4) #5. (2k+7)(k-2)

Explanation:

For #3 you have to first get all the terms on one side of the equals sign and set it equal to 0. So that gives us

`x^(2) -11x+28=0`.

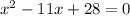Our a value is 1 and our c value is 28, so the product of those is 28. Find the factors of 28 and the combination of those factors that add up to equal the linear term -11x is the combination we need for our problem. The factors of 28 are: 1, 28; 2, 14; 4, 7. 4 and 7 give us 11 when we add them, but since we need a -11, we have to use the negative of both the factors since -7 + -4 = -11. Set up your equation now using the -7 and the -4, "larger" number first (the absolute value which makes the 7 larger):

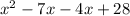`x^(2) -7x-4x+28`. This is the pattern that you will use to factor the next problem, as well.

Group the terms in groups of 2 to get:

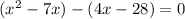`(x^(2) -7x)-(4x-28)=0`. Notice the sign change in front of the 28 in the second set of parenthesis. This is because if I distribute the negative infront of the parenthesis back in, negative times a negative will give us the +28 in the original problem. The same will apply again in #5 when we get there.

Now factor out whatever is common from each set of parenthesis:

`x(x-7)-4(x-7)=0`.

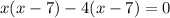Now the common term is the factor (x-7) so that can be factored out now, leaving behind:

(x-7)(x-4). That's the answer for #3.

Now for #5:

We will start by getting everything on one side (I am changing the k's to x's):

`2x^(2) +3x-14=0`.

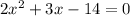The product of our a value and c value is again 28. Find the combination of the factors of 28 that will add to give us the middle (linear) term of 3: That is again 7 and 4, with the 7 needing to be positive and the 4 needing to be negative since 7 - 4 = 3. Set up our expanded quadratic as follows, "larger" number (the absolute value of) first:

`2x^(2) +7x-4x-14=0`.

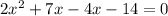Group them into groups of 2 again:

`(2x^(2) +7x)-(4x+14)=0`

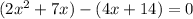
Again, notice the necessary sign change so when we distribute the negative back into the parenthesis we get the -14 we started with in the original problem.

Now factor out what is common from each set of parenthesis:

`x(2x+7)-2(2x+7)=0`.

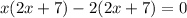What's common now is the factor (2x+7) so that can be factored out leaving behind

(2x+7)(x-2)=0

And you're done!!!