2 Answers

Intgr · Answer 1 · 2020-05-15T01:50:45+0000

For this case we must find an expression equivalent to:

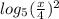
$log_ {5} (\frac {x} {4}) ^ 2$

So:

We expanded
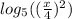$log_ {5} ((\frac {x} {4}) ^ 2)$ by moving 2 out of the logarithm:

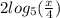
$2log_ {5} (\frac {x} {4})$

By definition of logarithm properties we have to:

The logarithm of a product is equal to the sum of the logarithms of each factor:

log (xy) = log (x) + log (y)

The logarithm of a division is equal to the difference of logarithms of the numerator and denominator.

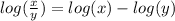
$log (\frac {x} {y}) = log (x) -log (y)$

Then, rewriting the expression:

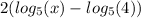
$2 (log_ {5} (x) -log_ {5} (4))$

We apply distributive property:

$2log_ {5} (x) -2log_ {5} (4)$

Answer:

An equivalent expression is:

$2log_ {5} (x) -2log_ {5} (4)$

Please log in or register to add a comment.