Question

A cabin cruiser travels 48 miles upstream (against the current) and 48 miles downstream (with the current). The speed of the current is 4 miles per hour. Find the total time traveled if the cabin cruiser travels at 12 miles per hour in still water.

Answer 1

Hello!

The answer is:

The total time traveled by the cabin cruiser is equal to 9 hours.

Why?

To solve the problem, we need to write two equations using the given information about the travel upstream and downstream.

Then, we need to write two equations:

Let be "x" the speed of the cabin cruiser (12 mph in still water)

Let be "y" the speed of the current (4 mph).

So,

For the travel against the current (upstream), we have:

`(x-y)*t_(upstream)=48miles\\\\(x-y)*t_(upstream)=48miles\\\\(x-4mph)*t_(upstream)=48miles`

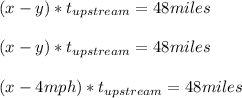
For the travel with the current (downstream), we have:

`(x+y)*t_(downstream)=48miles\\\\(x+y)*t_(downstream)=48miles\\\\(x+4mph)*t_(downstream)=48miles`

Also, we know from the statement that the speed of the cabin cruise traveling in still water is equal to 12mph.

So,

Calculating the time traveled upstream, we have:

`(x-4mph)*t_(upstream)=48miles(12mph-4mph)*t_(upstream)=48miles(8mph)*t_(upstream)=48milest_(upstream)=(48miles)/(8mph)=6hours`

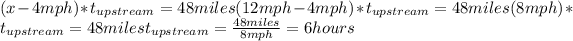
Calculating the time traveled downstream, we have:

`(x+4mph)*t_(downstream)=48miles(12mph+4mph)*t_(downstream)=48miles(16mph)*t_(downstream)=48milest_(downstream)=(48miles)/(16mph)=3hours`

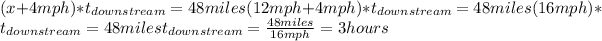
Now that we know the time traveled upstream and downstream, we need to calculate the total time traveled using the following equation:

`TotalTime=t_(upstream)+t_(downstream)\\\\TotalTime=6hours+3hours=9hours`

Therefore we have that the total time traveled is equal to 9 hours.

Have a nice day!