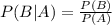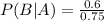Question

At the Rolling Ridge School spelling bee, 75% of the

contestants advanced to the second round and 60% advanced
to the third round. What is the probability that a randomly
selected contestant advanced to the third round given the same
contestant advanced to the second round?
A. 3/20
B. 9/20
c. 7/15
D. 4/5

Answer 1

Answer: Option D

`P (B | A) =(4)/(5)`

Explanation:

Call A to the event in which a student advances to the second round.

We know that:

`P (A) = 75\% = 0.75`

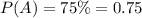
Call B the event in which a student advances to the third round.

We know that:

`P (B) = 60\% = 0.6`

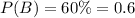
We then look for the probability of B given A. This is:

`P (B | A) =(P(B\ and\ A))/(P(A))`

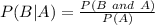
In this case, the probability of B and A is equal to the probability of B, since the students who advance to the third round also advanced to the second round before

`P (B | A) =(P(B))/(P(A))`

`P (B | A) =(0.6)/(0.75)`

`P (B | A) =(4)/(5)`