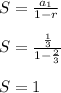Answer:
The equation is:
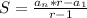
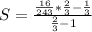
The sum is:

--------------------------------------------------------------------
If the sequence is infinite, the formula is:
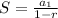
-------------------------------------------------------------------
Explanation:
We must calculate the radius of the geometric series
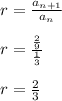
The first term of the series is:
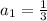
The last term of the series is:
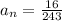
If the sequence is finite then the formula is:
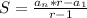
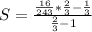

If the sequence is infinite then by definition as the radius are
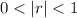 then the formula for the sum of the geometric sequence is:
then the formula for the sum of the geometric sequence is: