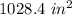1 Answer

Bioukh · Answer 1 · 2020-06-07T20:07:04+0000

For this case we have that if the box is cubed, then the volume is given by:

V = l ^ 3

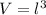
Where:

l: It's the side of the cube

We have to:

$l ^ 3 = 2244\\l = \sqrt [3] {2244}\\l = 13,09204886$

So, l is the side of the box. The surface area of a cube is given by:

$SA = 6l ^ 2\\SA = 6 * (13.09204886) ^ 2\\SA = 1028.41046012$

Rounding off we have that the surface area of the cube is:

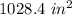
$1028.4 \ in ^ 2$

Answer:

$1028.4 \ in ^ 2$

Please log in or register to add a comment.