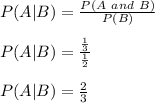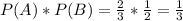Question

The Venn diagram shows the results of two events resulting from rolling a number cube.

Find P(A | B).

P(A) × P(B)
P(B)
P(A)

Answer 1

P(A) x P(B)

Explanation:

If im wrong, im so sorry

Answer 2

`P(A|B)=(2)/(3)`

`P(A)*P(B)=(1)/(3)`

`P(A) =(2)/(3)`

`P(B) =(1)/(2)`.

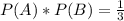
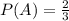
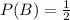Explanation:

We use the Venn diagram to calculate the desired probabilities.

Note that there are 6 possible results in the sample space

S = {1, 2, 3, 4, 5, 6}

Then note that in the region representing the intercept of A and B there are two possible values.

So

`P (A\ and\ B) = (2)/(6) = (1)/(3)`

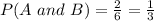
In the region that represents event A there are 4 possible outcomes {4, 5, 1, 2}

So

`P(A) = (4)/(6) = (2)/(3)`

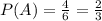
In the region that represents event B there are 3 possible outcomes {1, 2, 6}

So

`P(B) = (3)/(6) = (1)/(2)`.

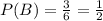Now

`P(A | B)=(P(A \ and\ B))/(P(B))\\\\P(A | B)=((1)/(3))/((1)/(2))\\\\P(A|B)=(2)/(3)`

`P(A)*P(B)=(2)/(3)*(1)/(2)=(1)/(3)`