Question

27 yd
36 yd
What is the length of the hypotenuse?
C-
yards

Answer 1

The length of the hypotenuse is: 45 yards

Explanation:

Given

a=27 yd

b=36 yd

To Determine

Hypotenuse = c

Pythagorean Theorem

For a right-angled triangle with sides a, b, and c is defined as:

`c=√(a^2+b^2)`

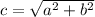
as

a=27

b=36

so substituting a=27, b=36

`c=√(27^2+36^2)`

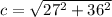
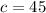`c=45` yards

Therefore, the length of the hypotenuse is: 45 yards