Question

Which choice is equivalent to the quotient below shown here when x>0?

Answer 1

For this case we must simplify the following expression:

`\frac {\sqrt {16x ^ 3}} {\sqrt {8x}} =`

Join the terms in a single radical:

\
`\sqrt {\frac {16x ^ 3} {8x}} =\\\sqrt {\frac {8 * (2x ^ 3)} {8x}} =\\\sqrt {\frac {2x ^ 3} {8x}} =\\\sqrt {2x ^ 2} =\\\sqrt [n] {a ^ m} = a ^ {\frac {m} {n}}`

So:

`\sqrt {2x ^ 2} =\\x \sqrt {2}`

Answer:

Option B

Answer 2

Choice B is correct

Explanation:

The given radical division can be expressed in the following form;

`\frac{\sqrt{16x^(3) } }{√(8x) }`

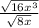
Using the properties of radical division, the expression can be expressed in the following form;

`\sqrt{(16x^(3) )/(8x) }=\sqrt{2x^(2) }`

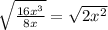
Simplifying further yields;

`\sqrt{2x^(2) }=√(2)*\sqrt{x^(2) }=x√(2)`

Choice B is thus the correct alternative